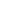A User’s Guide for Non Rocket Scientists (Part 1)
by Terry Burlison
Note: A glossary of terms is provided at the end of the article.
NASA has flown rendezvous missions for nearly a half-century. Since Project Gemini, astronauts and mission controllers have safely brought space vehicles together, whether from one country or more, over the earth or the moon, in a matter of hours or of days. They make it look as easy as calling your best friend and saying, “Meet me at Costco at ten o’clock.”
How do they make this astonishing feat look so easy? What does it really take to get a vehicle from the launch pad into orbit and mated safely with another craft, hundreds of miles high traveling at a blistering 18,000 miles per hour?
Well, sit down, strap in, and hold on. You’re about to learn why it’s called “rocket science.”
The “panes” of rendezvous
Planning a rendezvous mission starts months, even years before the actual flight. Seemingly as much art as science, rendezvous dictates when you launch, where you launch from, how long the mission lasts, how much propellant you need, and when your crew eats and sleeps. It can be constrained by sunbathers in Cuba or Hawaii, the location of the sun, foreign birth-control programs, or a human’s vomiting tendencies.
But it all starts with the question, “When do we leave?”
During a mission countdown, in real-life or even in the movies, one often hears of a launch window: a mysterious slice of time during which the spacecraft must leave the pad. (In movies, this is usually right before a hurricane hits.) Any mission that involves rendezvous, whether with the International Space Station (ISS) or with another planet, has a launch window: a scheduled liftoff time and some additional duration, often only a few minutes long, during which you must launch. For low earth orbit (LEO) missions, this window is defined by two limitations or “panes”: the planar pane and the phasing pane. (Windows have panes, get it? That passes for NASA humor.)
A low earth orbit is essentially a circular path around the earth. (Actually it’s elliptical, but that’s one of several complications we’ll ignore for this discussion. Okay, it’s not eactly elliptical, either, but . . . never mind.) If you draw a big circle on a flat piece of cardboard you’ll notice that the circle lies in a plane. When a vehicle is in orbit, it remains within its orbital plane. If you somehow launched into the wrong orbital plane, you are, in NASA parlance, SOL (“shit out of luck”). A simple diagram will explain:
Figure 1: One degree of orbit plane change (not to scale)
Once you’re in orbit, traveling at about 18,000 mph (27,000 km/hr), changing your direction even a little takes a LOT of delta-V (change in velocity). To change your orbital plane by one degree requires a maneuver of over 400 feet (122 meters) per second. For the space shuttle, this would require nearly half of the shuttle’s entire on-orbit maneuvering capability, which must be also used for attitude control, orbital maneuvering, rendezvous and docking, separation, and deorbit.
(Note: That’s why the shuttle Columbia couldn’t have just “gone to the ISS” had they known about the wing damage. Such a massive plane change would have taken about 12,000 feet (3,700 meters) per second of delta-V!)
Thus, it is really, really, really important to get into the correct orbital plane at launch. This is where the planar launch pane comes in.
In LEO, your orbital plane remains fixed relative to the stars; it does not rotate along with the earth below. (This is another simplification, but true enough for the moment.) Imagine cutting a big circle in your sheet of cardboard, drawing an arrow to indicate direction of travel, and placing this cardboard “orbit” around a globe, one of those desktop models you can spin. Place it so the arrow is pointing counter-clockwise when viewed from the north pole. Be sure the center of the orbit always coincides with the center of the earth.
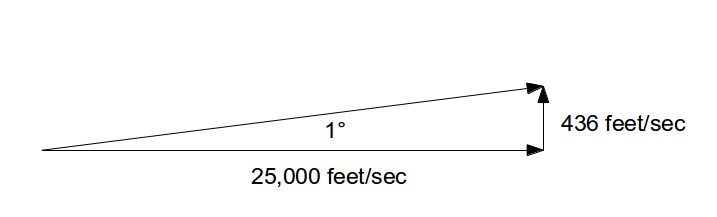
If your cardboard lies along the equator (or “equatorial plane”), the inclination of the orbit is said to be zero degrees. You’re always flying over the equator. This is creatively referred to as an equatorial orbit. Now if you tip your cardboard up to a 51.6° angle to the equator, still keeping the centers aligned, you’ve set your orbit at an inclination of 51.6°—which happens to be the inclination of the ISS. The two points where the plane intersects the earth’s equatorial plane are the ascending (northward) and descending (southward) nodes.
Figure 2: Orbital inclination and line of nodes (Source: NASA's RNDZ 2102 Workbook)
As mentioned earlier, the orbital plane does not rotate; it remains fixed while the earth rotates beneath it. If you pick a spot on the earth, say at the Kennedy Space Center in Florida (28.5° latitude) and spin your globe, you’ll notice that the launch site passes directly through the plane of your cardboard orbit twice per day.
Thus begins the definition of the launch window.
Two times each day, your launch site will pass directly under the plane of your target orbit. This is when you must launch! If you delay, you will be launching into a different orbital plane; even if it has the same inclination, it will cross the equator at a different point and create a wedge angle between the orbits. Since the earth rotates 360° in 24 hours, elementary school math tells you that’s a degree every 15 minutes. Very quickly, you’ll be too far out of plane to ever make your rendezvous.
But it gets worse. It also turns out you typically don’t have two opportunities per day. Virtually all launch sites in the world have some kind of launch azimuth restriction, defined by range safety considerations. Simply put, there are some launch angles you can’t use because your rocket will be flying over populated areas. Launching too far northward out of Cape Canaveral, for example, overflies the east coast of the United States, an area rife with politicians and lawyers who will take monetary offense if you drop empty stages or solid rocket boosters on them. Launching too far southward, the path passes over Cuba and the Bahamas. Since there are a number of catastrophic failures, from explosions to engine failures, that could cause a booster to plummet to earth in a horrific fireball, good neighbor policies forbid flying over those populated areas, as well. Thus, northward flights from Cape Canaveral are limited to an inclination range of 28.5° (due east launch) to about 57°.
(Note: To get into higher inclination orbits, including polar orbits, the United States actually launches southward out of Vandenburg AFB in California.)
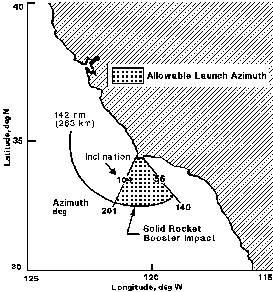
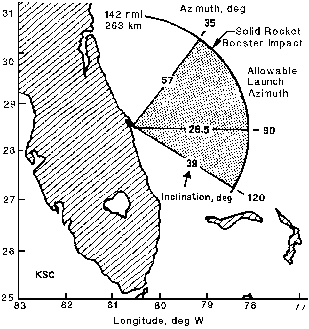
Figure 3: Launch azimuth constraints for Vandenburg AFB (Western Test Range) and KSC (Eastern Test Range)
As you might have noticed in the above figure, there exists a small range of inclinations, 28.5° to about 38°, that do have two opportunities a day out of KSC, north and south. But since the ISS orbits at an inconvenient 51.6° (more on that later), a vehicle launching from KSC has only one launch opportunity per day, launching to the north.
Therefore, once a launch date has been chosen by mission planners, the launch time is now fixed: For the ISS, it’s the time on that date that KSC will rotate under the northbound (or ascending) segment of the ISS orbit plane.
Sadly, launching on time has long been a problem in the space program, especially for the shuttle. That’s why countdowns have all those built-in holds; they provide time for the launch team to troubleshoot any problems before the scheduled liftoff. Even then, reliably launching on time is a tremendous challenge. Hence the need for a launch window.
But how long is the window? If we don’t launch exactly on time, how much propellant (and therefore, delta-V) is onboard our spacecraft for changing planes once on orbit? Essentially, none. But that doesn’t mean the vehicle must lift off at exactly the scheduled time, because of a technique used during ascent called yaw steering.
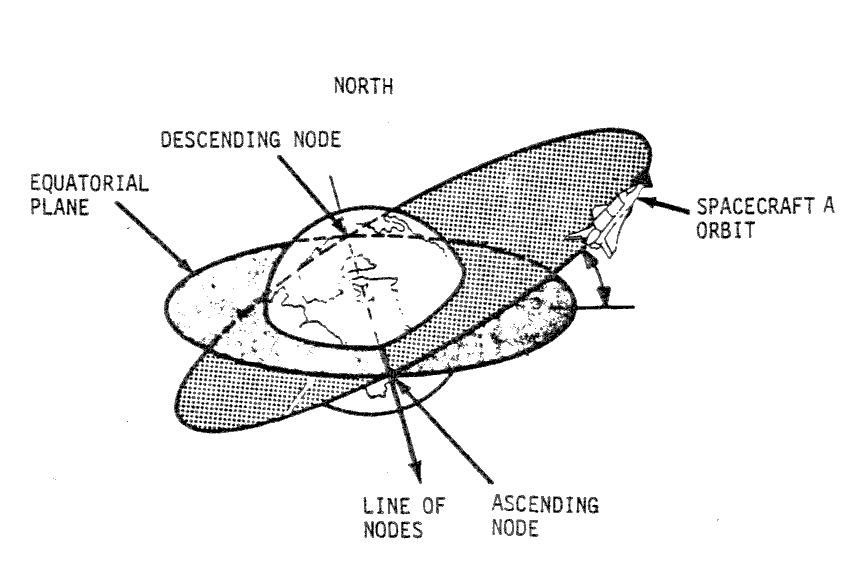
A dog-leg to the left (or right)
The launch vehicle imparts a massive amount of delta-V to the spacecraft, taking it from only a few hundred feet per second (the earth’s rotational velocity at the launch site) to some 25,000 fps (18,000 mph or 27,000 kph) at orbit insertion. Anyone who has seen a launch in person will testify to the awe-inspiring spectacle of millions of pounds of highly-explosive propellants erupting in pillars of flame and shattering the sky with ear-splitting power.
Typically, the spacecraft doesn’t require exactly 100% of that impulse to get into orbit: there is usually some extra capability, or margin, available. Planners can also reduce the payload to orbit in order to free up propellant during ascent. This margin can be used to turn the rocket in a “dog-leg” maneuver to get it into the correct orbital plane. This means the rocket can launch a few minutes early, or late, and still steer onto the right course. A vehicle’s “yaw-steering” capability depends on the rocket, the payload, and other factors, but for the shuttle, this amounted to about 10 minutes of launch window when flying to ISS. Additional yaw steering could be achieved by using more launch propellant to yaw, but this further reduces the payload you can lift into orbit. (For shuttle, a 10-minute launch window already costs about 2,500 pounds (1,100 kg) of payload.) Also, more extreme yaw maneuvers induce higher aerodynamic loads on the shuttle and its huge external tank and also affects downrange safety margins, such as where the external tank will impact after being jettisoned.
Figure 4: Illustrative dog-leg ascent (not remotely to scale)
Consequently, by sacrificing about 2,500 pounds (1,100 kg) of payload to orbit, the shuttle could launch about 5 minutes before the perfect time, or 5 minutes afterward, and still steer into the correct orbital plane, thus saving the vehicle’s onboard propellant for orbital maneuvers.
But where in the launch window is the best time to go? It depends on who you ask.
Figure 5: Shuttle launch window performance margin (Figure courtesy of Wayne Hale)
Oops
This anecdote, from a source that requests anonymity, illustrates the difference between science (the “perfect” answer) and engineering (the “best” answer).
“The FDOs (Flight Dynamics Officers) always set us up to launch at the opening of the window so we had the best chance of launching. However, that isn’t really the optimal position. [A certain astronaut] found out there were a couple of pounds of propellant to be saved by launching 6-7 minutes into the 10 minute window. He pressed this for over a year and finally won. So, we rock up to STS-88, the first launch to ISS. We have a system failure in the final 10 minutes before launch, it takes us too long to fix and get back on the count and we miss the launch by about 4-5 seconds. Window closes, launch scrubbed . . . because of a poor plan.”
As others have noted, the perfect is the enemy of the good.
Thus we have the “planar pane” of the launch window. But there is another constraint, one defined by surprisingly human limitations.
Going through a phase
When you launch, the odds are slim that your target vehicle, such as the ISS, will be in exactly the correct spot in its orbit for you to go right up and dock with it. Most likely, it will be too far ahead or behind. Thus, you could launch into the correct orbital plane and directly to the correct altitude, and discover your target is on the other side of the earth.
Mission planners could postpone the mission until a day when the target is in the perfect spot at the exact launch time, but a much better solution is to allow the chaser spacecraft to phase, or catch up to, the target spacecraft after launch.
A basic tenent of orbital mechanics dictates that the higher the orbit, the slower the orbital speed, whether it’s a satellite around the earth or a planet around the sun. It’s why a martian year is longer than an earth year. Thus, the target vehicle will be moving slower than a spacecraft at a lower altitude. The greater the difference in altitude, the greater the difference in speed. The lower, faster spacecraft thus catches up to the higher, slower one at a rate that depends on the heights, or energy, of their respective orbits.
It’s often not practical to raise the target vehicle to a higher altitude, nor can a chaser spacecraft safely orbit lower than about 100 nautical miles (185 km) altitude because of our atmosphere. Therefore, the chaser altitude range of 100 nm up to the target’s altitude defines the range of “catch-up rates” for chasing and rendezvousing with the target.
(Note: You could launch the chaser into a higher, slower orbit and let the target vehicle catch up to it and then rendezvous from above, but this is a waste of energy and therefore, of propellant, payload, and money.)
So when you get into orbit, the target will be some fraction of an orbit ahead of you, possibly close to 360°. This distance is called the phase angle. The lower the initial, or phasing, orbit, the faster the catch-up rate and the less time it takes to complete the phasing.
Now we add in the human element.
In the “good old days” of Gemini, the spacecraft was so simple that the crew could transition from launch to rendezvous almost immediately upon reaching orbit, and the rendezvous could be completed very quickly. (Gemini 11 achieved rendezvous on the first orbit!)
Figure 6: Gemini 11 rendezvoused with an Agena upper stage in one orbit (NASA archive photo)
The shuttle, however, was a vastly more complex machine, requiring a great deal of crew activity after launch to get everything configured for on-orbit activities: powering down auxiliary power units, opening payload bay doors, deploying the cooling radiators, etc. The crew had already been up for a long time and gone through the adrenaline-pumping experience of launch. Thus, NASA did not ask the crew to perform the time-consuming and difficult task of closing on the target vehicle and docking on the first day.
However, spaceflight experience has shown that space adaptation syndrome (“space-sickness”) is most likely to strike crew members on the second day. Since it’s distracting to use sophisticated navigation equipment while vomiting, rendezvous was typically scheduled to occur on day three, roughly 40 hours after launch.
As Ken Young, a retired NASA manager puts it: “The STS crew workday was heavier [than Gemini/Apollo]—open payload bay doors, deploy radiators, etc.—and with six or seven crew the chances of one or more being [nauseated] doubled or tripled, which drove the third day choice. But also it gave a much bigger phasing window (even though for Space Station visits at 51.6 the plane window was still only about 10 minutes).”
Additionally, allowing extra time for a vehicle to phase increases the number of launch opportunities per year. For example, if the vehicle has enough time on orbit to phase a full 360°, the ISS could be anywhere in its orbit on launch day, meaning any day of the year would potentially be feasible for launch.
So the crew planning people look at day three, determine when the crew will wake up, eat, and be ready to execute the final maneuvers, and align that (if possible) with the workday on the ISS. They also estimate how long it will take to perform those approach maneuvers and subtract that from when the crew needs to “call it a day” and get to bed. Those few hours in-between define the timeframe in which the phasing must be completed.
For example, assume the crew will awake at 0600 Greenwich Mean Time (GMT) on day three. Maybe two hours later, or 0800, they’ll be ready to fly the approach. If the crew must end their work day by 2300, the phase window would be fifteen hours long. However, that fifteen hours excludes the time it takes to approach and dock. If that requires ten hours (including some margin for contingencies), then the phase window is only five hours long, and phasing must be completed between 0800 and 1300 on that day.
Mission planners now come up with the rendezvous profile: the orbital altitudes and durations that will bring the chaser spacecraft to the ISS within the window defined above.
That’s if everything goes right. If there is a launch delay, however, the original phase angle between the chaser and the ISS—the one mission planners worked so hard to estimate and then used for all the mission timeline planning—will change. This changes the amount of phasing time required and can cause the ISS crew to violate the wake/sleep constraints. For example, a delay of 10 minutes means the ISS will have moved almost 40° further ahead in its orbit. This could require the chaser to phase too long and put the rendezvous too late in the day three workday. Consequently, there exists a “phase pane” in the launch window that limits the amount of launch delay to assure that the chaser will arrive at the target on the correct day, and within the correct timeframe on that day.
It is the intersection of these two panes that defines the final launch window.
To summarize: mission planners pick a launch day, which gives a nominal lift-off time. This time is then moved slightly earlier according to how much yaw-steering the booster rocket can do. This is the opening of the launch window. Crew timeline impacts are studied to determine the best arrival time and the phasing constraints are added to the yaw-steering limits, giving the closing of the launch window.
All that just to get off the ground.
Just change the laws of physics
Other considerations can impact the launch window, such as lighting conditions at launch. Since the shuttle could abort its ascent and land across the Atlantic (or even back at the Cape), launches were scheduled when lighting conditions from the sun were such that the crew could clearly see the runways. After the Columbia accident, NASA also required certain lighting conditions for the cameras observing the shuttle during ascent. Thus, a poor sun angle for a given day/time could also impact the launch window.
A source who prefers to remain anonymous recounts the following story about the preliminary plan to fly cooperative rendezvous missions with the Russians in the early 1990s.
Ronald Reagan had proposed building Space Station Freedom: an entirely U.S. asset, launched due east from Kennedy Space Center into a 28.5° inclined orbit. This would maximize the size of the station we could build, since launching eastward takes full advantage of the earth’s rotational speed. Due-east launches also allow for relatively long launch windows. (Take my word for that.)
Bill Clinton scrapped Freedom and redirected NASA to build a station in partnership with the Russians. As part of a live-together-before-marriage arrangement, NASA was directed to fly missions to the Russian Mir space station, which was at 51.6° inclination. This meant not only reducing our payload capability to orbit, but drastically shortening the launch windows, because of the orbital plane issues discussed earlier.
My source recounts a press conference given by NASA Administrator Dan Goldin shortly after signing the agreement: “A very funny story about that was Dan Goldin was doing a press conference right after we had signed all the agreements with the Russians for the Mir missions, and someone asked about the short launch windows and the potential for missing a launch due to a failure close to launch. Goldin, in his typical humble self, declared that a 10-minute launch window was unacceptable, he had never approved it, and he would get that changed. We almost fell out of our chairs laughing. We never did get the answer as to whether he was going to move the Sun or the Mir. Neither moved and we lived with 10 minute launch windows throughout Mir and ISS.”
Birth control vs. détente
Yet another launch constraint we haven’t discussed is communications coverage—the requirement for key events in the mission (radio, radar tracking, video, etc.) to happen during certain times or over certain locations. Ken Young relates the following story about the 1975 Apollo-Soyuz Test Project (ASTP), the first cooperative space mission between the U.S. and the Soviet Union.
In 1974, NASA launched an Applications Technology Satellite (ATS-6), a spacecraft that would provide much better tracking of the upcoming ASTP mission. The satellite was to be placed in geosynchronous orbit over the Galapagos Islands.
Young explains: Unfortunately, unbeknownst to us planners (and, indeed, to all but a few NASA people) the State Department had made a commitment to India that in mid-1975 the ATS-6 would be re-located to about 35 degrees East (over equatorial east Africa) to support a year-long Indian birth-control education program. The Indian government gave out hundreds of black and white TV sets, with antennas that could pick up birth-control videos beamed down from the ATS-6 to little villages.
This little surprise came just [a few] months before the July 1975 flight. Thus, re-planning of the whole . . . sequence was required. The rendezvous and subsequent handshake [the famous “handshake in space”] would now have to occur over France, in the ATS-6 new coverage zone. That, as only rendezvous experts will understand, also meant a significant liftoff time change to accommodate the optimum terminal phase lighting conditions. Needless to say, ASTP officials on both sides were not happy with such a “last-minute” change. Such things as the schedule for live congratulatory talks from President Ford and Chairman Brezhnev had to be changed [as well]. And remember, every detail of ALL plans had to be documented in both English and Russian and run through the interminable sign-off gauntlet, a process that literally took months. Then NASA had to negotiate through the State Department to allow for several days during the actual flight that India would not use the ATS-6 to transmit their birth-control videos.
Despite all the uproar we managed to make the changes and pull off a perfectly nominal rendezvous, docking and crew transfer with excellent live TV coverage. I don’t think anyone ever examined Indian birth statistics nine months after the days we used ATS-6, but chances are they’d find a spike in births!
Figure 7: Planned parenthood from orbit: NASA's ATS-6 satellite (NASA archive image)
Getting there from here (wherever “here” is)
Once you’ve figured out when to launch, you have to figure out how you’ll actually find and approach your target vehicle. Rendezvous can be broken into two segments: the inertial segment and the relative segment. When the chaser vehicle gets on-orbit, the target is typically far, far ahead, out of sight, way beyond the range of any kind of rendezvous radar. So the first several maneuvers are planned by the ground, which is tracking both vehicles and knows where they are in inertial (Earth-centered) space. Once the chaser gets into close proximity, it can acquire the target with its own sensors, radar for example, and then figure out the best way to get to it. This is the relative phase—when the chaser can measure where the target is relative to its own position. It’s rather like using your GPS to get you to the mall, then using your eyes to get into the parking lot and finding a space.
Theoretically, the chaser could stay in its low initial parking orbit until just the right moment and blast its way up to the ISS, but as discussed before that would most likely cause rendezvous too soon. Regardless, such a maneuver generates very high closing rates. Coming in at high speed is very dangerous, as the crew has little time to respond to problems or errors, and a 200,000 pound (91,000 kg) spacecraft hardly handles like a sports car. Additionally, stopping “quickly” requires blasting all the chaser’s reaction control system (RCS) jets directly at the target, spraying it with all kinds of nasty rocket contaminants (plume impingement).
Imagine parking in a tight space at the mall. You could roar down the parking lot at full speed, slam on the brakes at the last second and throw your car into the spot. After all, it works in the movies. But in the real world we slow down as we turn in, slow down even more as we approach our spot, then very slowly and carefully turn the vehicle into the spot and creep up to the correct position before stopping.
So too, in orbit.
Therefore, to ensure arrival at the right time, with the right lighting conditions, and with low closing velocities, our rendezvous profile consists of a series of maneuvers to gradually raise the chaser’s orbit, each one reducing the closing rate, and culminating in an approach to the target at the right time and place.
It can look something like this:
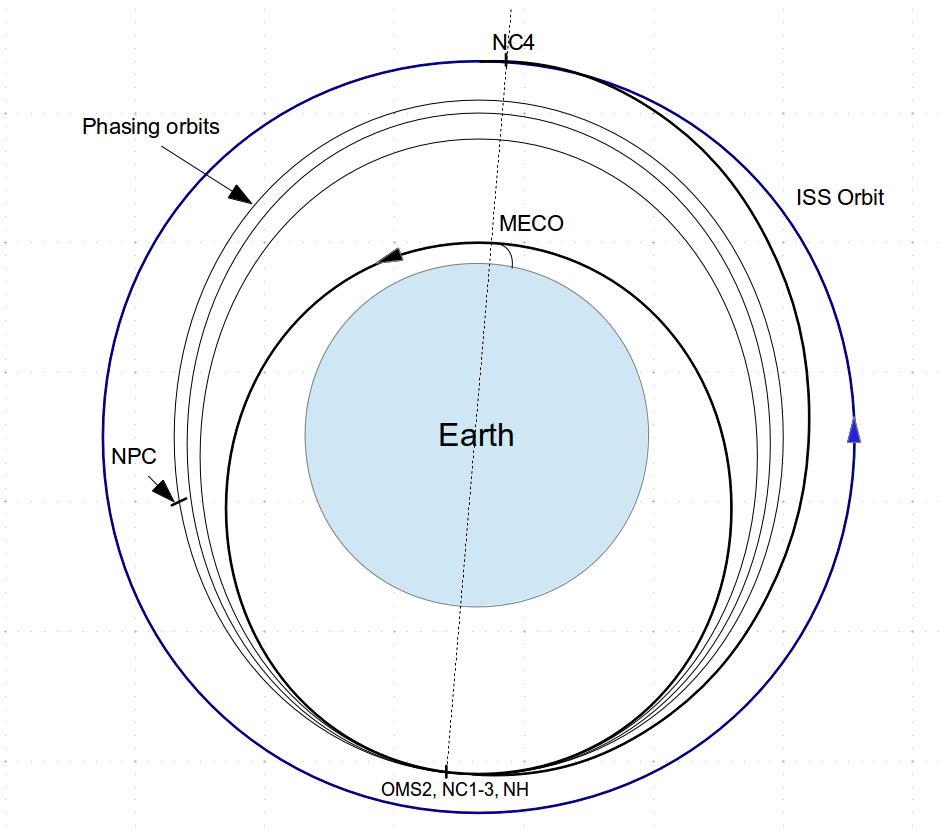
Figure 8: Sample shuttle rendezvous profile (inertial view from above ISS orbit plane)
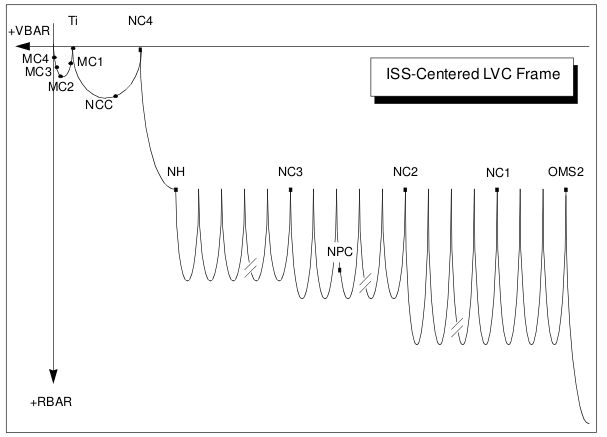
Figure 9: Sample shuttle rendezvous profile (relative view centered at ISS)
(Source: Rendezvous and Proximity Operations Design Reference for the International Space Station)
These graphs show an approach of the shuttle to the ISS. The upper is an inertial view of the maneuvers, looking down from a point above the target orbit plane. The lower graph uses a relative coordinate system, centered at the ISS with the vertical axis pointing downward toward the center of the earth and the velocity direction to the left.
As you can see, the profile consists of a series of oddly-named maneuvers that gradually raise first one “side,” then the other, of the shuttle’s orbit, until finally reaching the ISS orbital altitude.
Let’s go through the maneuvers.
The OMS2 burn occurs immediately after orbit insertion to place the shuttle in its parking orbit. On the ground, Mission Control recomputes the rendezvous profile after they’ve determined the shuttle’s precise orbit (and allowing for any launch delay). So while the maneuvers themselves will stay in the profile, for now, their timing and magnitude will change slightly.
The first “phasing” burn, called NC1, is performed to raise the apogee (highest point) of the shuttle’s orbit. This increases the orbit’s period, slowing down the catch-up rate to the ISS. These coasting phases can last for many hours, even days.
The shuttle will adjust this phasing orbit multiple times, in this case NC2 and NC3, each tweaking the shuttle’s apogee and catch-up rate. During one of these coast phases, the shuttle might perform small planar correction burns (NPC), to correct for any errors in the launch that did not place the orbiter in precisely the desired orbital plane and resulted in a wedge angle between the vehicles’ planes. Recall that even small planar errors can result in very large burns.
On rendezvous day, the shuttle executes a maneuver designed to bring it to the ISS’s vicinity. The height adjust (NH) raises the apogee of the shuttle’s orbit to a specified height, in this case the altitude of the ISS. A half-orbit later, the shuttle performs another phasing burn to take it right on in to the terminal rendezvous phase.
The shuttle might also have stopped at the NC4 point on the plot before approaching. If berthing is to be postponed for several hours (or a day or more), this “stand-off” distance may be as much as 40 nm (74 km) or more behind the ISS, where the shuttle can drift safely while the crew sleeps.
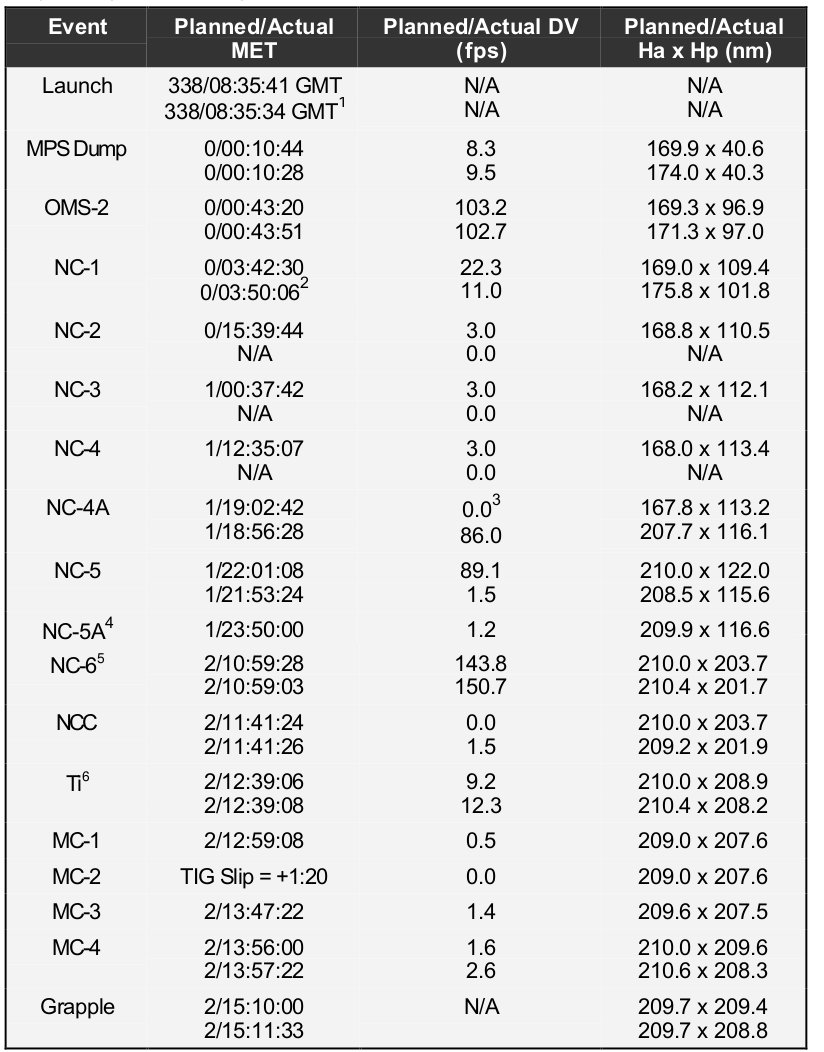
A nearly infinite number of profiles can be employed to perform a rendezvous, each with advantages and drawbacks. NASA flew many different profiles during Gemini, Apollo, Skylab, ASTP, and shuttle. The profile above was developed for shuttle mission planning purposes. An actual profile, as flown on STS-88 to Mir, is shown below. Note the large number of (mostly small) NC (phasing) maneuvers. These as-flown maneuvers are the result of constant updates of the shuttle and Mir locations which caused the Flight Dynamics Officer to re-compute the profile during flight, substituting NC maneuvers for the originally planned burns.
Figure 10: STS-88 actual rendezvous profile, as flown (Source: STS-88 Post-Flight Report)
Fly me to the . . . ISS
Now that we see how it’s done, let’s hop aboard an imaginary vehicle and go through a rendezvous mission.
Mission planners have picked a date and time for us to arrive, accounting for ISS crew schedules, ground coverage (Russia requires the rendezvous occur over the Motherland), lighting, etc. Working backward, they have determined the launch date and thus, the launch time. The launch window has been calculated, and all systems are Go.
We climb aboard our fictional space vehicle, which we’ll call the space shuttle. A small problem delays launch by three minutes, but we’re still well within our window when the main engines ignite, the solid rocket boosters erupt, and six million pounds of thrust blast us into our parking orbit. Because of the delay, the ISS is about 12° further ahead in its orbit than we had planned. If we stick to our original rendezvous plan, we’ll have to spend more time in our phasing orbits and will arrive too late in the Day 3 workday.
No worries. After NASA has tracked our vehicle for a while to be sure they have a good fix on our position and velocity, Mission Control’s Flight Dynamics Officer (FDO, call sign “Fido”) calls upon his back-room support people and together they update the rendezvous maneuvers to get us to the ISS when and where we should. They send us the updated maneuver plan, changing the burn times and amounts slightly to correct for errors from launch and to allow for the longer phasing time.
Over the next two days, we’ll keep getting these updates from Mission Control. As burns are executed, the FDO will change the rest of the plan based on new tracking data. Small plane-change maneuvers may be inserted to correct for errors from launch or other factors. Over those two days the ISS, originally far on the other side of the earth, becomes visible ahead and above us, a beacon gleaming in the sunlight, far brighter than any star or planet. Slowly, it brightens further, climbing closer and (apparently) higher as we move toward it. If we need to, we could now use our star tracker, normally used to align the inertial platform in our vehicle (more on that later), to track the angles to the ISS. Using algorithms known as Kalman filters, we can check our relative position to the ISS (even though we’re still in the inertial rendezvous phase) to make sure that everything is on course.
On day three, we are finally ready to rendezvous. We’ve gotten the latest updates from Mission Control and fire the first of two burns to get us up to the ISS orbit. The ISS grows larger, brighter, closer. We pass into darkness and can no longer see it, but a light on the ISS gleams in the blackness, surrounded by innumerable, brilliant stars. As we approach daylight, the ISS suddenly blossoms into brilliance as the sun hits it. Moments later, a rainbow of color explodes along the horizon and we, too, pass into sunlight. We fire the final burn to raise our orbit to the ISS’s altitude, targeting a stand-off point behind it. As we coast up to the ISS altitude, the TIG (time of ignition) clock counts down to zero and the engines fire, gently pushing us back in our seats. Moments later, we have arrived: co-orbital with the ISS, some 40 nm (74 km) behind. Mission Control informs us that the burn was nominal (NASA-ese for “okay”) and we breathe a huge, collective sigh of relief.
We’re here. It’s been three long days, several maneuvers are behind us, and we are safely rendezvoused with the ISS, drifting behind it in a nearly identical orbit. All that remains now is to close from our stand-off point, fly-around for inspection, then approach and grapple.
We’ve accomplished the hard part (launch window targeting), the really hard part (ascent and rendezvous), and in next month’s installment, we’ll take on the really, really, really hard part: bringing our 100-ton vehicle safely to berth with the million-pound station, both tearing around the earth at 18,000 mph.
Sounds like fun!
Glossary
Ascending node: The intersection of a vehicle’s orbital plane with the earth’s equatorial plane, with orbital motion in a northward (versus southward or “descending”) direction.
Cross coupling: The translation motion caused by a rotational jet firing (and vice versa) caused by misalignment of the maneuvering jets to the vehicle’s body axes and center of gravity.
Delta-V: Change in velocity, caused by maneuvers or forces acting on the vehicle.
Doppler shift: The compression or stretching of an electromagnetic signal’s wavelength caused by motion toward or away from the observer.
Ephemeris: Essentially, a huge table predicting the positions, velocities, and other data of an object in orbit.
Equatorial orbit: An orbit around the equator, with 0° inclination.
Flight Dynamics Officer (FDO, “Fido”): The front-room Mission Control position responsible for the vehicle’s trajectory, from tower clear until landing and rollout. This includes all rendezvous maneuvers.
Geosynchronous orbit: An orbit with a period of 24 hours. If it is also a circular orbit at 0° inclination, the spacecraft remains fixed over the same spot on the earth (geostationary orbit). Primarily used for communications satellites.
Inclination: The angle of a satellite’s orbital plane to the earth’s equator.
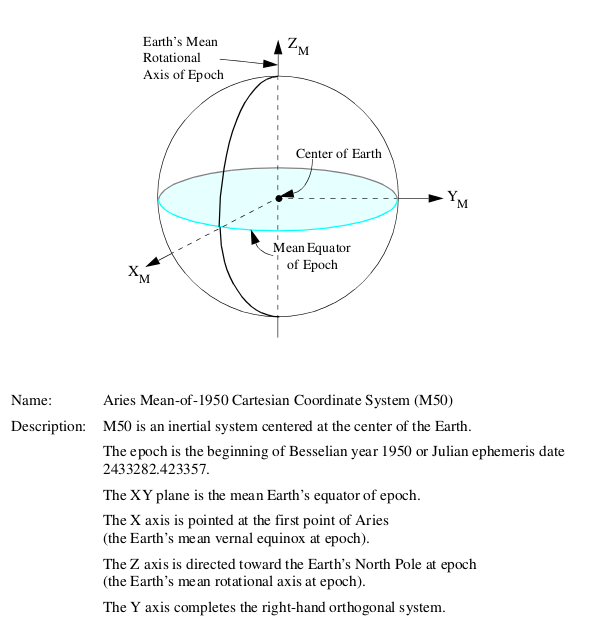
Inertial coordinate system: A non-rotating, essentially fixed (relative to the stars) coordinate system with origin at the center of the earth.
Figure 1: M50 Inertial coordinate system
(Source: Rendezvous and Proximity Operations Design Reference for the International Space Station)
Inertial Navigation System (INS): Avionics hardware used to calculate estimates of a vehicle’s state (position, velocity, attitude) relative to an inertial coordinate system.
Integrate: Computing the future state of a vehicle given its current state and estimates of future forces acting upon it.
Kalman filter: A mathematical algorithm that uses a series of measurements observed over time to estimate other variables that can’t be directly measured, or cannot be measured accurately.
Launch azimuth: The angle of a vehicle’s launch groundtrack, relative to due east.
Launch window: The time period on launch day during which a vehicle must launch to meet its mission objectives.
Launch window planar pane: The limitation on the launch window caused by the earth’s rotation and limited by a vehicle’s ascent performance.
Launch window phase pane: The limitation on the launch window caused by rendezvous constraints, such as lighting, communication coverage, or crew work day limits.
Lighting constraints: Limitations imposed by sun angle. Can impact launch, aborts, landing, on-orbit rendezvous, or approach and docking.
Margin: A vehicle’s capability beyond the minimum required to meet mission requirements, such as extra propellant, payload, time, etc.
Nodal regression: The westward (or eastward) rotation of a satellite’s orbital plane, caused primarily by the oblateness of the earth.
Nominal: Normal or expected.
Oblateness (Earth): The flattening of the earth, caused by our planet’s rotation and resulting in a “bulge” around the equator.
Phantom plane: The targeted insertion plane for the chaser vehicle which will result in minimal wedge angle difference at rendezvous.
Phase angle: The angle between the chaser and target vehicle, typically measured in the target vehicle’s orbital plane.
Phasing orbit: A chaser vehicle’s orbit, usually at a lower altitude (energy) from the target, causing it to approach the target over time.
Plume impingement: The impact of exhaust gases upon another object.
Relative coordinate system: An orthogonal, rotating coordinate system centered at one vehicle (usually the target) with the Z-axis pointing to the center of the earth, Y-axis along the satellite’s angular momentum vector, and X-axis perpendicular to both, with positive in the direction of orbital travel. For a circular orbit, X is along the velocity vector. Also called an LVLH (local vertical, local horizontal) coordinate system.
Figure 2: Relative coordinate system
(Source: Rendezvous and Proximity Operations Design Reference for the International Space Station)
Relative navigation system: Hardware, such as rendezvous radars or star trackers, used to measure angles, distances, velocities, or attitudes of one vehicle relative to another.
Rendezvous profile: A series of maneuvers designed to bring a vehicle from orbital insertion to the near-proximity of another spacecraft already in orbit.
Star tracker: An optical device for keeping an inertial navigation system properly aligned by measuring the positions of stars. Can also be used to track other objects in orbit.
State vector: A set of information describing the position, velocity, and attitude (and possibly rates) of a vehicle at a specific time.
State vector update: A new, more accurate state vector uplinked from the ground to improve the onboard estimate of a vehicle’s state.
Wedge angle: The angle between two orbital planes. A combination of the differences in inclination and ascending node location.
Yaw steering: A technique used during ascent to steer the launch vehicle to the east or west in order to get it into the proper phantom plane.
Zonal and tesseral harmonics: Higher-order effects of the earth’s non-spherical shape, which perturb the motion of vehicles in orbit.
Copyright © 2014 by Terry Burlison
Terry Burlison worked in mission operations at Johnson Space Center in the early days of the space shuttle program. He trained as the first shuttle-era rendezvous Flight Dynamics Officer (FDO), defined the Phase B RTCC (Real Time Computer Complex) rendezvous requirements, and designed rendezvous displays for use in the Mission Control Center. After leaving NASA, he worked for Boeing Aerospace and as a private contractor, developing automated rendezvous techniques for low earth orbit. He finished his career as a private consultant for various companies looking to resupply the International Space Station, including Rocketplane-Kistler, winner of one of the COTS (Commercial Orbital Transportation Systems) contracts in 2006 for ISS resupply. Terry is now a full-time writer, trying to get his articles and novels to rendezvous with his deadlines. You can follow Terry on Twitter at: @ExNASATerry, or post questions about this article on his blog here.